Welcome To Transit Performance Engineering

TRANSIT PERFORMANCE ENGINEERING * The Center Of Excellence For Public Transit Management and Technology

	Published in Carson City, Nevada, by Design & Development Engineering Press for Transit Performance Engineering

	Volume 5, No. 16	March 1994 Reading Level: General Public Professional
	BUFF LOADS FOR LRVs IN THE USA ARE TOO HIGH
	It was some five years ago, when we worked on a specification for the Baltimore LRV, that it first occurred to us that there was something wrong with the level of buff loads specified for light rail vehicles in the USA. As a reminder, the buff load is a design load that engineers apply to the ends of the car to squeeze it longitudinally for the purpose of either strength calculations or testing. The idea is that under the action of the specified buff load the car shouldn't change its shape permanently. What are the Buff Loads Specified for LRVs? While federal or unequivocally accepted buff loads standards are nowhere to be found, the 2g practice (i.e. specifying the buff load equal to 2 weights of the empty car) appeared until recently to be taking greater and greater hold in this country. Why, we may ask has this been happening? At least some possible explanations could be these: First, the only documents known to us that broadly regulate the problem of the buff load clearly specify it at the level of 2g's. The "Light Rail Transit Car Specification Guide" published in 1981 by N.D. Lea and Associates, Inc., a Washington D.C. consulting firm, specifies on page 3-2 of section 3.4 a horizontal design load applied at the end sills equal to two times the empty car weight. Another document, Order 143-A of the California Public Utilities Commission, requires (section 6.03, page 10) that this load be equal to twice the unladen car	body weight applied longitudinally at the end sills. This latter stipulation leads us to the other most likely reason for the persistence of 2g in our specifications: true to the proverb that as California goes so goes the nation, the evidence of California regulations always has a strong impact on buff-load considerations. We felt uneasy about these values for the buff load, and we made a number of calculations (see our newsletter "ADA and the LRV Design Buff Load", Volume 3, No 12, June 1992). We compared the weights and operational speeds of various trains: mainline commuter, rapid transit, subway, and light rail vehicle trains, and we ended up with something that we called "relative resistance to crash". We found that in terms of the forces and dissipated energy that may occur in collisions, American LRVs are much stronger than other types of rail vehicles. One may ask, what is wrong with that? What is wrong is that our LRV's might be too stiff, too rigid, and this in turn may hurt people when, during a collision where there is no adequate cushioning effect provided by the collapsing structure, they will be violently thrown against the elements of the vehicle interior. How did this happen? What led to such a situation? We want to show in this newsletter that one reason for this excessive LRV car body stiffness is the fact that for LRVs, and only for LRVs,

transit performance

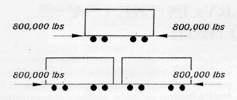
the buff load is not specified as an absolute force but as some fraction of carbody weight. In American practice. LRV specifications don't indicate that the buff load should be so many pounds. We say: it should be twice (or some other number) its empty weight. And this creates a problem.

Buff Loads of Other Cars

Let's start our comparison with mainline and commuter cars. The specified buff load for commuter cars is 800,000 lbs.

various weights, depending on their type and application. The book by Seymour Kashin and Harre Demoro, "The PCC Car, An American Original", page 190, gives the following weights of the early PCC cars:

Brooklyn 1001 _ 33.360 lbs, Chicago 4002 _ 36,400 lbs, St. Louis 1500 _ 33,620 lbs.

The Mystery Of the Original PCC Cars

Unfortunately, we have not succeeded in establishing the buff load of the PCC cars. It appears that all the original documents have been lost. Typical findings of our long search are well summarized in a letter we received from our friends at the Toronto Transit Commission: "Research here revealed a 1947 PCC specification document, but all reference to body and frame design referred to Transit Research Corporation documents which are not on file. It seems that TRC issued instructions and drawings required to build cars, but design criteria was known only to TRC. Sorry, Bill Brown." Still, the legend persists that it was on the original PCC cars that the concept of the 2g buff load was first introduced. We never found any confirmation of this. One tortured line of inquiry led us as far as Holland. There, Mr. J.K. Diekhuis, who was in the years 1967-1989 the technical director of the Hague transit authority, was the only one who could speak with authority about the buff loads on PCC cars: he developed one of their existing specifications, purchased the cars and used them through the fifties until eighties. His cars, however, were built to European standards of 200 kilo-Newtons (or approximately 43,300 lbs.) buff load, and this doesn't reflect our North American experience.

Nevertheless, for the sake of the present argument let's assume that the PCC buff load indeed was equal to twice the weight of an empty car (2g).

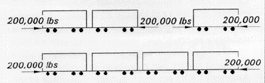
Please notice that this requirement remains constant irrespective of the number of cars in a train consist. Thus, whether there will be two cars, five, or ten in the train consist, a single car has to resist the same 800,000 lbs.

The same logic applies to rapid transit cars with their 200,000 lb buff load requirement. Whether for a single car, or a consist of two, four or more cars, this strength requirement remains the same.

Now, what about LRVs? The predecessors to contemporary LRVs, the original PCC cars, had

	Unit Weight		Train
Description	Car	Locomotive	Weight	Maximum Speed		Speed Square	Kinetic Energy	Buff Load	Crash Index
	(lb)	(lb)	(lb)	(mph)	(fpsec)	(fpsec)square	(ft-lbf)	(lb)	(lb/ft-lbf)
					(5) x 1.46	(6) x (6)	(4)x(7)/2/32.2		(9)/(8)
Column (1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
4LRVs	90,000		360,000	50	73	5,329	2.98E+07	180,000	6.04E-03
10 Rapid Transit Cars	85,000		850,000	75	110	11,990	1.58E+08	200,000	1.26E-03
10 Commuter Cars + 2 Locos	120,000	400,000	2,000,000	95	139	19,238	5.97E+08	800,000	1.34E-03

3	transit performance

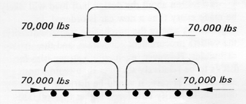
	Thus, the buff loads for the cars listed above had presumably been: for Brooklyn - 66,720 lbs., foe Chicago - 72,800 lbs., and for St. Louis - 67,240 lbs. Therefore, let's assume that the buff load of the PCC cars averaged approximately 70,000 lbs. On occasion, these cars were coupled in pairs or in multiple-unit trains, as seen in the pictures in the previously mentioned book, "The PCC Car, An American Original", for instance on pages 82, 105, 108, and 110. No evidence is to be found that on these occasions transit authorities went through massive structural modifications to multiply the buff load of these cars by the figure representing their number in a train consist. This was the same policy as described earlier in respect to main-line and mass-transit cars.	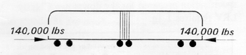two, three, or more - will lead to further increase of buff load requirements. Time For a Change Let's illustrate this problem with a little exercise. A Sacrament U2 articulated LRV with a length of 80 ft weighs 80,000 lbs. Let's take a train consisting of two such units. There is some simplification in the reasoning that follows, but let's agree for a moment that if the bodies of the Sacramento vehicles are split into rigid halves the new smaller vehicles would be half the present length and weight, 40 ft long at 40,000 lbs. Applying the rule of 2g buff load they would be built to a squeeze load of 80,000 lbs. A train of four such cars would also have a strength corresponding to 80,000 lbs buff load. Now, if four of these hypothetical cars were modified and all connected with articulation joints, the resulting unit would weigh 160,000 lbs, and we would be required build it to a buff load of 320,000 lbs. Two trains of the same length, weight, function and performance,

	This was held to until the concept of articulation become popular for reasons of reduced operational cost. Then, suddenly, a unit which should have been considered as consisting of two car bodies, was treated as a single car with the resulting extreme increase of design buff load!

	Please notice that what is being challenged here is not any particular value for the buff load but the practice of doubling this value when a coupler joint between cars is replaced by an articulation joint. A concern may be voiced that adding more articulations in future designs for the U.S. market -

4	transit performance

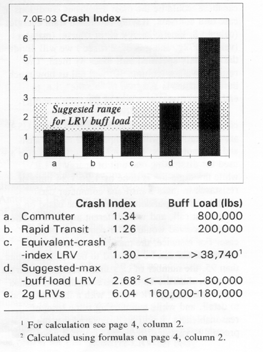
	one requiring 80,000 lbs squeeze strength, the other 320,000 lbs, the only difference between them being the presence of articulations in the stronger one! In view of the examination conducted above it appears quite reasonable that the convention of defining buff loads as a function of LRV weight be abandoned once and for all. We recommend that the LRV car body design squeeze force be specified in terms of an absolute load, similar to requirements in the USA for rapid transit and commuter rail cars, and for LRVs elsewhere in the world. What Should the Specified Buff Load Be? It is suggested that to answer this question we compare (see table, bottom of pages 2-3) the kinetic energies of three of the heaviest train sets for each of the main rail vehicle, namely LRV, rapid transit and commuter cars, each train set running at the highest possible operational speed. For each type of car these would be the most disastrous conditions in case of a collision. Having calculated train energies (column 8; kinetic energy is, of course, (mass) x (velocity)2/2g, and g is 32.2 ft/sec2) we will divide the presently specified buff loads by them. The resulting values (column 10) will tell us how much buff resistance is assigned to "handle", i.e. to endure and disperse, a unit of the train's energy. The analysis shows (see diagram, page 3, column 4) that the car bodies of LRVs in the USA are underutilized when compared to mass transit and commuter cars. 6.04 units of buff resistance are used for dissipating one unit of energy in LRVs while the same job is done by 1.26-1.34 units of resistance in mass transit and commuter cars. Such a comparison will always be based on a judgement call, and with different assumptions the results received would differ somewhat in each case. For instance, the maximum speed of the commuter car can be assumed to be 100 mph rather than 95, the number of cars in the rapid transit train 12 rather than the 10 used here, or the cars loaded rather than empty. However, with a little attention to detail, and while maintaining some level of reasonableness, it will be discovered that the presently existing differences identified among the types of cars investigated remain in roughly the same relation: the expected collision performance of rapid transit and commuter cars will be comparable; that of LRVs - quite different.	Interesting question: what would the LRV buff load be if the car were required to have the same Crash Index as rapid transit and commuter cars? This can be calculated as follows: Since that Crash Index = (Buff Load) / (Kinetic Energy), then the Buff Load (Crash Index) x (Kinetic Energy). Thus, if the desired Crash Index for LRVs is to resemble those for mass transit and commuter cars, i.e. to be approximately 1.3E-03, therefore the equivalent buff load for LRVs would be (for energy value see table, pages 2-3): (Buff Load)LRV=2.98E+07 x 1.3E-03=38,740 lbs A decision about the design buff load will likely be made every time a new car is ordered, in negotiations among the purchasing transit authority, the vehicle procurement consultant, and the carbuilder. However, even with a strong bias for LRVs to be relatively stronger than rapid transit and commuter cars, it would be difficult, in our opinion, to justify buff loads higher than 60,000-80,000 lbs. This is certainly true for the LRV train set investigated here, consisting of four 85,000-90,000 lbs. cars, and capable of speeds up to 50-55 mph. It may be expected that the LRVs ordered in the USA in the near future will be showing this trend toward lowering the specified buff loads. For instance, the latest (1994) low-floor car specification prepared for the downtown Chicago LRV requires 1.1g

		transit performance is a newsletter published on an irregular schedule by Transit Performance Engineering, and is devoted to selected news and views from world-wide developments in high-efficiency public transit systems and equipment. Elizabeth Eva Lewalski, PE, President Transit Performance Engineering 110 East Ann Street, Suite E Carson City, Nevada 89701 Tel. (702) 883-2164 FAX (702) 887-1321 Copyright by Transit Performance Engineering. All rights reserved. ISBN-0-944327-04-7